Chapter 10 Binary regression: Data with more than one trial per row

So far, the dataset we used for binary regression had one “trial” per row: there was a categorical variable in the dataset with two categories, “success” and “failure” (for the frogs: Abnormal and Normal). We wanted to estimate the probability of “success” as a function of several predictors.

If there are multiple trials that all have the same predictor-variable values, we can group them together into one row of data, and just record the number of “trials” and the number of “successes”. (From this, we can also get the number of “failures” = “trials” - “successes”, if needed.) If we have a dataset that is stored in this format, we can still use glm() to fit a binary regression model. The R code to fit the model changes just a bit, and we are able to do better model assessment a bit more easily.

An example follows.

10.1 Data

The dataset used here is a reality-based simulated EIA dataset on duck sightings before and after windfarm installation (impact). Hourly, observers did up to 200 scans of the study area, and for each scan recorded whether duck(s) were seen (a success) or not (a failure).

The data file can be accessed online at:\

##   successes trials day month impact
## 1       172    200   7     1      0
## 2       190    200  13     1      0
## 3       191    200  27     1      0

10.2 Checking the data setup

We would like to model the proportion scans with ducks sighted as a function of a set of covariates. Each row of our dataset gives us the number of successes in some number of trials (and also gives the corresponding values of the covariates for ALL those trials). We can also use this kind of summary data with a logistic regression; we will just need to add a column for the number of failures:

pd <- pd %>% mutate(failures = trials-successes)
#or same thing in base R
pd$failures = pd$trials - pd$successes

10.3 Fitting a saturated model

Let’s try fitting a model for proportion sightings as a function of day, month, and impact.

We need a response “variable” that is really 2 variables bound together: a column with the “successes” and a column with the “failures”. These don’t have to be literally called successes and failures – you can use whatever variable names you like – but the first one of the two should be successes (the thing you want to compute the proportion for) and the second failures.

duck.logr <- glm( cbind(successes, failures) ~ day + month + impact, 
                  family=binomial(link='logit'),
                  data=pd)
summary(duck.logr)

## 
## Call:
## glm(formula = cbind(successes, failures) ~ day + month + impact, 
##     family = binomial(link = "logit"), data = pd)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -4.272  -1.344   0.235   1.312   3.618  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  2.77029    0.07710   35.93  < 2e-16 ***
## day         -0.01173    0.00356   -3.29    0.001 ** 
## month       -0.09155    0.00782  -11.71  < 2e-16 ***
## impact      -0.22264    0.04841   -4.60  4.2e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 488.19  on 71  degrees of freedom
## Residual deviance: 244.96  on 68  degrees of freedom
## AIC: 607.9
## 
## Number of Fisher Scoring iterations: 4

#or maybe...
duck.logr2 <- glm( cbind(successes, failures) ~ day + factor(month) + impact, 
                   family=binomial(link='logit'), 
                   data=pd)
summary(duck.logr2)

## 
## Call:
## glm(formula = cbind(successes, failures) ~ day + factor(month) + 
##     impact, family = binomial(link = "logit"), data = pd)
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -3.783  -1.157   0.172   1.289   3.428  
## 
## Coefficients:
##                 Estimate Std. Error z value Pr(>|z|)    
## (Intercept)      2.61840    0.12370   21.17  < 2e-16 ***
## day             -0.01173    0.00406   -2.89  0.00383 ** 
## factor(month)2  -0.29734    0.13509   -2.20  0.02773 *  
## factor(month)3  -0.01429    0.14177   -0.10  0.91971    
## factor(month)4  -0.28787    0.13576   -2.12  0.03397 *  
## factor(month)5  -0.25836    0.14149   -1.83  0.06785 .  
## factor(month)6  -0.40456    0.13291   -3.04  0.00234 ** 
## factor(month)7  -0.14197    0.13921   -1.02  0.30780    
## factor(month)8  -0.45232    0.13229   -3.42  0.00063 ***
## factor(month)9  -0.63286    0.12826   -4.93  8.0e-07 ***
## factor(month)10 -0.66599    0.12979   -5.13  2.9e-07 ***
## factor(month)11 -1.13601    0.12384   -9.17  < 2e-16 ***
## factor(month)12 -0.94948    0.12800   -7.42  1.2e-13 ***
## impact          -0.22363    0.04852   -4.61  4.0e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 488.19  on 71  degrees of freedom
## Residual deviance: 197.84  on 58  degrees of freedom
## AIC: 580.7
## 
## Number of Fisher Scoring iterations: 4

10.4 Checking linearity

What should be linear here? Well, logit(p) (where p is the probability of success, for a given set of predictor-variable values) should be a linear function of the predictors. We can actually check this graphically now that we have multiple trials per row of data! (But remember that the effects of other, unplotted predictors may also be influencing the plot that you see…)

Here, we need to decide: Do we see a linear pattern (or no pattern)? For the month and day data here, we might also consider whetehr it would make more sense to fit either of them as a categorical covariate rather than numeric.

gf_point(logit(successes/trials) ~ day, data=pd) %>%
  gf_labs(y='logit(p)')
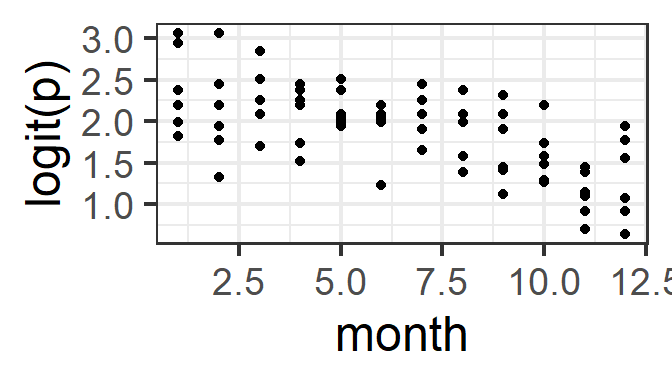
gf_point(logit(successes/trials) ~ month, data=pd)%>%
  gf_labs(y='logit(p)')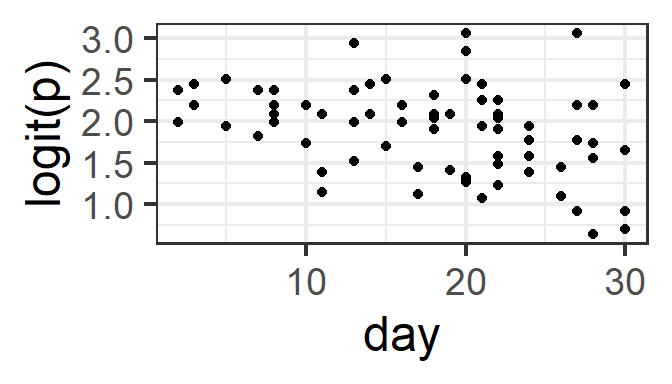

10.5 Model Assessment

With data set up as proportions (many trials with the number of successes and failures in each row, rather than one row per trial), model assessment plots are a bit more useful. Specifically, we can check the Pearson residuals vs. fitted plot for constant variance as a function of fitted value, to confirm that the mean-variance relationship matches what we expect.

Since the Pearson residuals are already adjusted for the expected variance, we should see approximately constant spread, with values ranging from about -2 to 2 (and not more than a few larger than \(\pm\) 3).

acf(resid(duck.logr2, type='pearson'))
gf_point(resid(duck.logr2, type='pearson') ~ fitted(duck.logr2))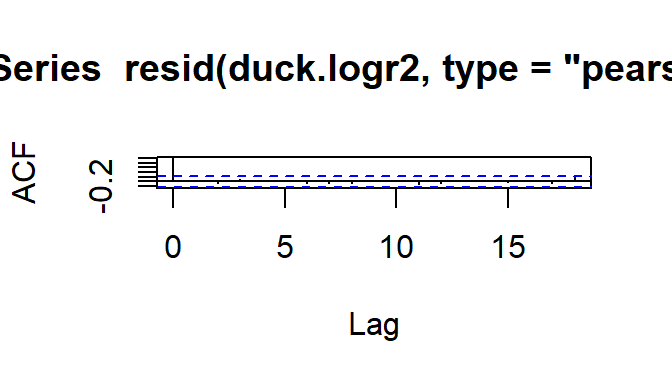

10.6 Model Selection

We can do model selection as usual. Here, it looks like the best model is the saturated (full) model.

require(MuMIn)
duck.logr2 <- update(duck.logr2, na.action='na.fail')
dredge(duck.logr2)

## Global model call: glm(formula = cbind(successes, failures) ~ day + factor(month) + 
##     impact, family = binomial(link = "logit"), data = pd, na.action = "na.fail")
## ---
## Model selection table 
##   (Int)     day fct(mnt)    imp df logLik AICc delta weight
## 8  2.62 -0.0117        + -0.224 14   -276  588   0.0  0.934
## 7  2.43                + -0.224 13   -281  593   5.3  0.066
## 4  2.50 -0.0117        +        13   -287  606  18.2  0.000
## 3  2.31                +        12   -291  612  23.6  0.000
## 6  2.44 -0.0285          -0.220  3   -372  750 161.8  0.000
## 2  2.33 -0.0284                  2   -382  769 180.6  0.000
## 5  1.92                  -0.219  2   -411  826 238.2  0.000
## 1  1.80                          1   -422  845 257.0  0.000
## Models ranked by AICc(x)

We might also try using model selection to help us decide whether to use quantitative or categorical month and/or day…

duck.logr2 <- update(duck.logr2, formula= . ~ . + month + factor(day), na.action='na.fail')
dredge(duck.logr2, rank='BIC')

## Global model call: glm(formula = cbind(successes, failures) ~ day + factor(month) + 
##     impact + month + factor(day), family = binomial(link = "logit"), 
##     data = pd, na.action = "na.fail")
## ---
## Model selection table 
##    (Int)     day fct(day) fct(mnt)    imp     mnt df logLik BIC  delta
## 14  2.62 -0.0117                 + -0.224         14   -276 613   0.00
## 30  2.62 -0.0117                 + -0.224         14   -276 613   0.00
## 13  2.43                         + -0.224         13   -281 617   4.11
## 29  2.43                         + -0.224         13   -281 617   4.11
## 26  2.77 -0.0117                   -0.223 -0.0916  4   -300 617   4.36
## 15  2.31                +        + -0.225         33   -238 617   4.57
## 16  2.34 -0.0146        +        + -0.225         33   -238 617   4.57
## 31  2.31                +        + -0.225         33   -238 617   4.57
## 32  2.34 -0.0146        +        + -0.225         33   -238 617   4.57
## 25  2.63                           -0.222 -0.1025  3   -305 624  10.97
## 6   2.50 -0.0117                 +                13   -287 630  17.05
## 22  2.50 -0.0117                 +                13   -287 630  17.05
## 5   2.31                         +                12   -291 634  21.15
## 21  2.31                         +                12   -291 634  21.15
## 18  2.65 -0.0117                          -0.0914  3   -311 634  21.31
## 7   2.19                +        +                32   -249 634  21.75
## 8   2.22 -0.0146        +        +                32   -249 634  21.75
## 23  2.19                +        +                32   -249 634  21.75
## 24  2.22 -0.0146        +        +                32   -249 634  21.75
## 27  2.88                +          -0.224 -0.1195 24   -268 638  25.44
## 28  2.91 -0.0134        +          -0.224 -0.1195 24   -268 638  25.44
## 17  2.51                                  -0.1023  2   -316 640  27.91
## 19  2.77                +                 -0.1193 23   -278 655  42.50
## 20  2.79 -0.0134        +                 -0.1193 23   -278 655  42.50
## 10  2.44 -0.0285                   -0.220          3   -372 756 143.77
## 12  2.35 -0.0310        +          -0.222         23   -336 770 157.12
## 11  2.29                +          -0.222         23   -336 770 157.12
## 2   2.33 -0.0284                                   2   -382 773 160.51
## 3   2.17                +                         22   -346 787 173.97
## 4   2.23 -0.0310        +                         22   -346 787 173.97
## 9   1.92                           -0.219          2   -411 831 218.12
## 1   1.80                                           1   -422 847 234.75
##    weight
## 14  0.360
## 30  0.360
## 13  0.046
## 29  0.046
## 26  0.041
## 15  0.037
## 16  0.037
## 31  0.037
## 32  0.037
## 25  0.001
## 6   0.000
## 22  0.000
## 5   0.000
## 21  0.000
## 18  0.000
## 7   0.000
## 8   0.000
## 23  0.000
## 24  0.000
## 27  0.000
## 28  0.000
## 17  0.000
## 19  0.000
## 20  0.000
## 10  0.000
## 12  0.000
## 11  0.000
## 2   0.000
## 3   0.000
## 4   0.000
## 9   0.000
## 1   0.000
## Models ranked by BIC(x)

Here it looks like day as quantitative and month as categorical works best.